The recent interest in NFTs has led to a large increase in spot volumes [1]. Peripherally to that, NFT lending markets have also started to appear and have grown rather rapidly in the past few months [2]. With no decent framework to price the interest rates on this demand for NFT debt, relatively large spreads have appeared. Here, we will try to identify what the correct interest rate is, which will hopefully help bring more liquidity and reduce spreads.
For some background, as of today, nonrecourse secured debt is the most commonly issued kind of credit in the NFT space. For example:
- Alice wants to borrow 30 ETH for 14 days at 5% interest and use her Punk as collateral.
- Bob sends Alice 30 ETH and Alice locks her Punk into the smart contract.
- Either Alice repays her loan, or she defaults:
- a. Alice repays 30 ETH + 1.5 ETH (5%) to Bob and she receives her Punk back.
- or b. Alice fails to repay 30 ETH + 1.5 ETH (5%) and Bob seizes her Punk.
In order to price an interest rate, we must somehow derive what the expected value of a loan is. Then once we can calculate this, we want to find an interest rate that results in an expected return of 0 for both the lender and the borrower. The first step in this process is to model the payoff function for the lender. That is quite easy:
The intuition behind this graph is that Alice will default on her loan if the spot value of her collateral is less than the amount that she owes: principle (30 ETH) + coupon (1.5 ETH). If she defaults, then Bob must liquidate the collateral. He will receive the current spot value. So when the spot value is below 31.5 ETH Bob effectively has the same exposure as if he were holding Alice's collateral directly.
One thing to note here is the similarity between this payoff graph and a put option payoff graph. It is an easy mistake to assume that the premium of a put option should therefore match the coupon payment on the loan. However the key difference between an option premium and a coupon payment is that the coupon payment is paid at the end, whereas the premium on a put option is paid at the start. This is a fundamental difference that will change the optimal interest rate by quite a bit. At the end of this article I'll show some comparisons with put option expectations vs nonrecourse loan expectations to illustrate the difference.
Now that we have a payoff graph, we have to calculate the expected value on a loan given some interest rate and some principle amount. We can break up this calculation into two distinct parts:
- If Alice repays what is the expected value weighted by the probability that this will happen?
- If Alice defaults what is the expected value weighted by the probability that this will happen?
Assuming a normal distribution of prices and a loan amount of 30 ETH, a current spot price of 35 ETH, a coupon payment of 1.5 ETH and a volatility of 10 ETH over the duration of the loan, then the probability that Alice will default is:
This is telling us what the probability is that after 14 days the price of Punks is going to be below 31.5 ETH.
Given this, it is quite easy to see what the expected value is if Alice does not default. It is simply the probability that Alice repays multiplied by the amount that Bob will receive:
Now lets calculate what the expected value is if Alice defaults:
If we sum these then we then can get Bob's expected value:
If we combine this all together then we can get a very nice looking graph. The green line is the sum of the expecation of default and repayment:
So we can see that the optimal coupon payment is 3.118 ETH (on a 14 day, 30 ETH loan, with 35 ETH spot price and 10 ETH volatility). This is because the expected value is 30 ETH when the coupon payment is 3.118 ETH - matching the original loan amount. Pretty neat.
If we run various simulations using the above loan terms and different coupon payments, the average payoff for a lender looks like this [3]:
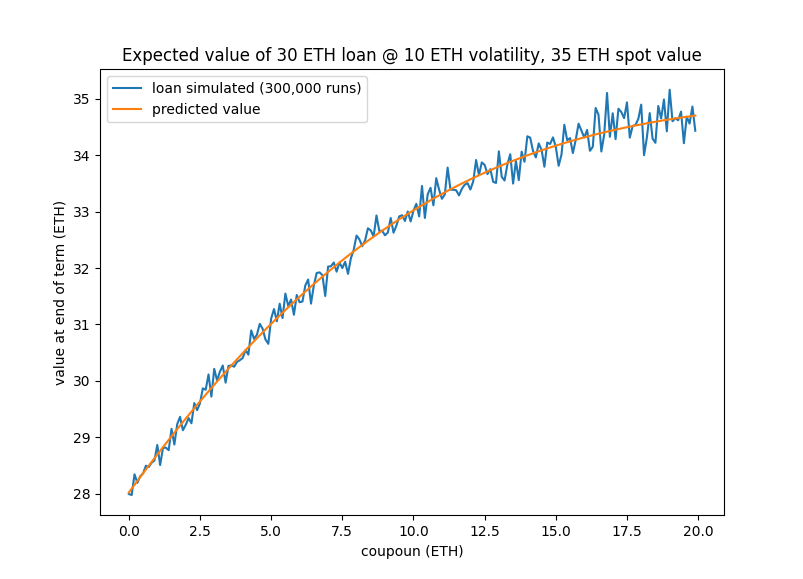
The simulations match up with the proposed formula. So we now have a framework to identify what the correct coupon payment is.
Lets now compare the expected value of a loan with the expected value for a put option and see where the difference lies. We'll use the same volatility (10 ETH), spot price (35 ETH) and a strike of 30 ETH to match the loan. Then running simulations on both instruments we can obtain the expected value of them at expiration [4]:
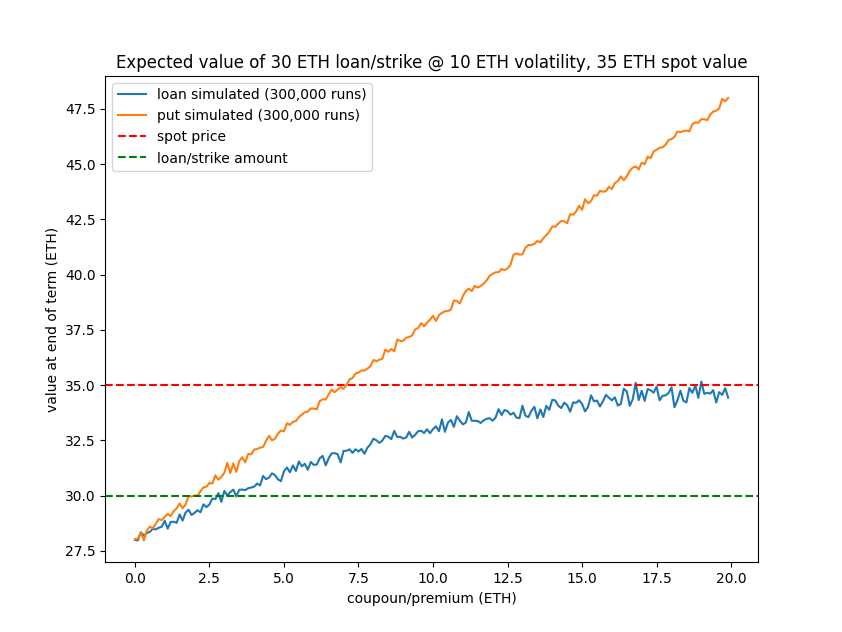
As we can see, for varying premiums, the expected value of a put option is quite a bit different from a nonrecourse loan. Again, the intuition behind this is that with a put option you get paid upfront whereas with a loan you get paid the coupon at the end. The coupon payment for a loan @ 30 ETH should always be priced higher than the premium for a put @ 30 ETH.
Something to note is that the expected value of a loan levels off as it approaches the spot value. If we think about it, this makes a lot of sense; as the coupon payment approaches infinity then the lender is guaranteeing a default. Based on the first payoff graph, we know that if a default happens the lender is exposed to the spot price of the NFT. So with a gauranteed default, the lender has effectively now taken on a spot position. Assuming a random walk, the expected price at T+n matches the current spot price (35 ETH). And so the expected value should never be higher than this - no matter how high the coupon payment is.
There are various things that can be improved upon here but this should act as a good starting point. The assumption that prices are normally distributed is not correct, the risk free rate and smart contract risk are not accounted for, and only a numeric solution for finding the optimal coupon is proposed here. These things would probably serve as good avenues to improve upon.